Prix Abel 2022

Prix Abel 2022

Les prix mathématiques

En¹ l’absence de prix Nobel dédié aux mathématiques, il existe non pas un mais deux prix pour distinguer les auteurs de contributions exceptionnelles à cette discipline : la Médaille Fields décernée tous les quatre ans à un mathématicien de moins de quarante ans pour une contribution remarquable et le Prix Abel attribué annuellement à un mathématicien sans considération d’âge afin de couronner une carrière exemplaire.

Cette année 2022, le prix Abel vient d’être attribué au mathématicien américain exerçant à New-York Dennis Parnell Sullivan pour ses contributions révolutionnaires à la topologie ainsi que pour ses capacités à élucider un large éventail de problèmes mathématiques en les observant à travers une loupe géométrique.

L’originalité d’une démarche

les sciences de l’espace

La topologie est une branche des mathématiques relativement jeune qui étudie les propriétés des «formes géométriques» et des «formes algèbriques» qui sont abstraites et générales (proximité, déformations, etc).

La géométrie algébrique, de son côté, unit géométrie et algèbre dans le sens où elle explore les relations existant entre les figures géométriques d’une part et les équations qui les décrivent d’autre part. Par exemple, dans le plan où les points sont repérés par deux coordonnées \(x\) (l’abscisse, horizontale) et \(y\) (l’ordonnée,verticale) le cercle centré en l’origine \((0,0)\) et de rayon \(1\) est décrit par l’ensemble des points dont les coordonnées \((x,y)\) vérifient l’équation \(\;(E)\;\colon\; x^2 + y^2 =1\). Ce cercle est appelé la variété algébrique associée à l’équation \((E)\).

Le grand avantage de la géométrie algébrique est qu’elle permet d’étudier les propriétés des objets géométriques (des variétés algébriques) à l’aide de calculs effectués sur leurs équations (manipulations algébriques sur les polynômes par exemple). Mais l’inverse peut également se révéler fructueux. On peut déduire des propriétés de certaines équations à partir des propriétés géométriques des variétés algébriques qui leur sont naturellement associées (avec des applications en cryptographie au travers des courbes elliptiques ou encore en analyse de grands ensembles de données)

Jeter des ponts entre les disciplines

Le mérite de D. Sullivan a consisté à constamment chercher à appliquer avec originalité les méthodes spécifiques à un domaine à un autre apparemment éloigné. Notamment des méthodes utilisées en géométrie algébrique à la topologie pour pouvoir calculer certaines propriétés des variétés (topologiques).

Les variétés topologiques sont des espaces topologiques particuliers (et importants) qui semblent «plats» lorsqu’on les regarde de près (ou qui localement ressemblent à un espace classique muni de coordonnées) mais qui, vus globalement, possèdent des propriétés plus complexes. La surface d’une sphère ou celle d’un tore sont des variétés de dimension \(2\) par exemple.

La méthode pour étudier de telles formes consiste classiquement à leur associer des objets algébriques appelés groupes d’homotopie qui en capturent les propriétés fondamentales. Malheureusement ces groupes sont difficiles à manipuler et les calculs qu’ils permettent sont extrêmement complexes.

En mathématiques, l’homotopie est une déformation continue entre deux applications, notamment celles qui décrivent des chemins ou des lacets (chemins fermés ou boucles). Leur étude est fondamentale pour la détermination des propriétés des variétés (d’un seul tenant ou «à trous» par exemple).

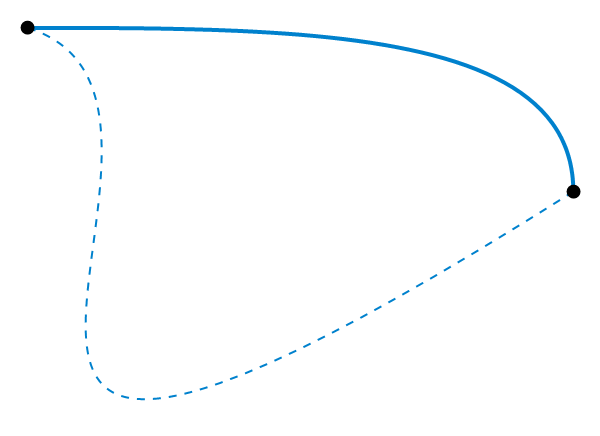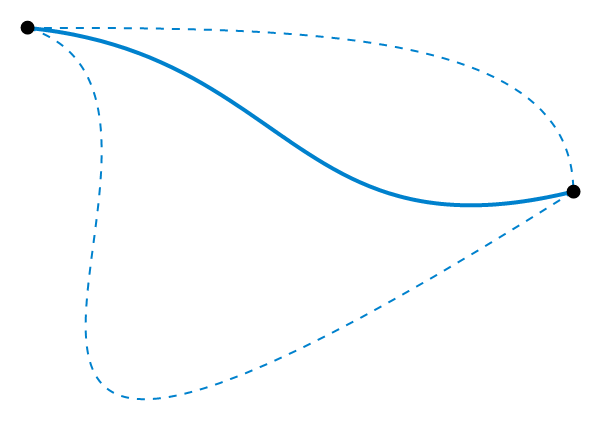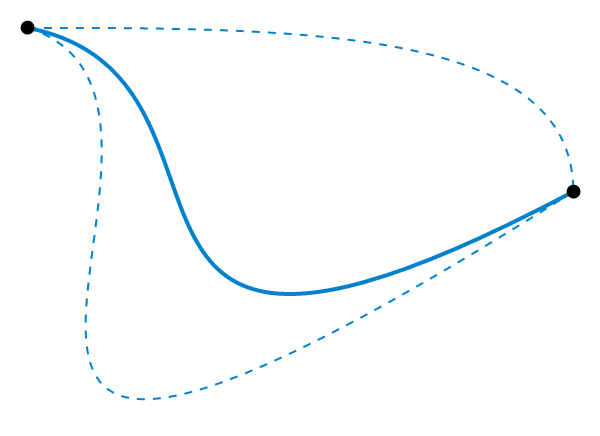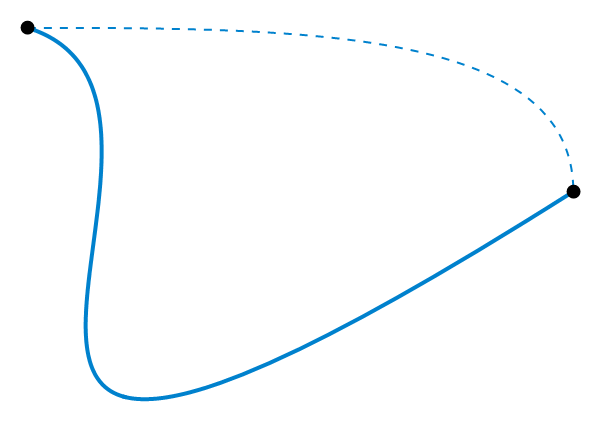
Déformation continue d’un chemin (crédit : Jim Belk).

L’apport de Dennis Sullivan

A la fin des années 70 D. Sullivan a joué un rôle fondateur dans l’élaboration de la théorie de l’homotopie rationnelle qui va permettre de rendre les calculs sur ces groupes d’homotopie plus accessibles, en laissant de côté certaines de leurs caractéristiques et en les associant non plus à des entiers mais à des rationnels, après avoir approfondit une méthode consistant à reconstruire une variété à partir d’une autre de manière contrôlée (chirurgie). Cette voie novatrice le mènera à une classification complète des variétés d’un certain type en dimension supérieure ou égale à 5 et à une avancée significative dans une conjecture concernant le «découpage» de telles variétés en morceaux constitutifs triangulaires.

Mais ce qui transparaît à travers ces travaux c’est bien la fascination profonde et essentielle qu’exerce sur D. Sullivan la nature première de l’espace et ce que l’on peut en découvrir en l’observant de différents points de vue : «Que signifie pour un espace d’avoir la structure d’une variété ?&#187.

En ce sens l’invention de ces techniques n’a constitué pour lui qu’une étape, un moyen de vérifier que la symétrie et d’autres propriétés de l’espace continuaient d’exister dans ce sens très local, divisé, dans le but de lui permettre d’atteindre des résultats encore plus généraux, qui, autrement, lui auraient échappés.

Les atomes de l’espace

Dans les années 80, Dennis Sullivan (qui entreprit des études de chimie avant de se réorienter vers les mathématiques) commença par adopter dans son étude des variétés ce qu’il a appelé un point de vue extérieur, plus global depuis lequel, par définition «la variété n’a pas réellement de personnalité locale, elle n’a pas de texture sur sa peau, pas de grain de beauté. Chaque lieu ressemble à n’importe quel autre…comme sur une flaque de lait.»

Sa motivation étant néanmoins la découverte de cette personnalité locale de l’espace, il s’orienta ensuite vers l’étude des systèmes dynamiques : «Un système dynamique possède des textures différentes en des parties différentes de la variété. La dynamique relevait vraiment d’un monde nouveau.»

Consacrés, comme leur nom l’indique, à l’étude du mouvement, de l’évolution de systèmes au sein d’un espace (comme l’évolution d’une population soumise à des contraintes de ressources, le modèle proie-prédateur ou bien encore la trajectoire d’un point du plan complexe soumis à l’action itérée de la fonction \(z\mapsto z^2 + 1\)) et dont certains exhibent un comportement chaotique, ils lui permirent de prouver une conjecture vieille de 60 ans (le problème de Julia-Fatou) sur la façon dont des points (et leur domaine environnant) de ce type de systèmes finissent par revenir à leur position initiale au lieu de «vagabonder» indéfiniment.

Pour prouver ce résultat (et d’autres encore dont un relié aux mathématiques sous-tendant une propriété universelle de certains systèmes dynamiques), il établit un rapport entre deux domaines auparavant séparés : l’étude des systèmes dynamiques générés par les itérations de fonctions et l’étude de certains groupes de symétries agissant sur une classe particulière d’espaces géométriques.

Dans les premières années du vingt et unième siècle, Dennis Sullivan revint au point de vue extérieur de la topologie qui caractérisa les débuts de sa carrière et développa, en collaboration avec Moira Chas une nouvelle méthode pour classer les variétés basée sur l’étude des chemins et lacets tracés sur leur surface.

Depuis cette époque ses recherches ont encore accentué l’association étroite qu’il entrevoit entre les systèmes dynamiques et la topologie par l’interprétation topologique des équations décrivant l’écoulement des fluides.

Comme le souligne Hans Munthe Kaas, un mathématicien enseignant à l’université de Bergen en Norvège et membre du comité du Prix Abel : «Je ne suis pas certain que Dennis Sullivan concoive les frontières entre les différents domaines des mathématiques de la même façon que les autres les envisagent.»

1. Librement inspiré de Jordana Cepelewicz ainsi que d’autres articles. ↩